Teak-nbtree

Introduction

Teak acronym for "Test Essential Assumption Knowledge". Know More

Essentially--Assume something, Focus on it, Prune rest and repeat

Nb-Tree is tree of tables as leaves. Each leaf has a naive bayes classifies running on its table of data. We can also run naive bayes on nodes(i.e. running on all of its child leaves)

Assumption : When a table is mapped on to an xy-plane. Similar rows are located closely to each other.

Note:In above sentence, closely refers to eucledian distance between two rows on an xy plane.

PS: I will be using xy-plane instead of a 2D-plane

Hypothesis

A table can be mapped onto an xy plane using this pretty little code:

row = any(data)
east = furthest(row)
west = furthest(east)
c = dist(east,west)
for each row r in data:
    a = dist(r,east)
    b = dist(r,west)
    x = (a^2 + c^2 - b^2)/2c
    y = (a^2 + x^2)^0.5    

Similar rows are grouped aka they are close to each other on the xy-plane.

1. We can increase the effectiveness of naive-bayes classifier by running it only on those similar rows that are close to the row that is to be predicted.
2. In order to increase efficiency of nb-tree, for a set of test rows I will generate a tree only once and get a list of tables(or leaves).
3. Efficiency will be considerably increased as we only need to measure distance between a row and a list of rows.
4. Then, I will determine which leaf is closest to each given test row.
5. Run a naive bayes classifier on it to get the accuracy.

Shown as:

for each row "t" in test:
        + Using cosine and Pythagoras, map the training data on xy plane.
        + tx,ty<----------Also map test row "t" on that same xy plane.
        + run xy.tiles to build a tree and get a set of leaves(tables)
        + xy_means_of_leaves=calculate mean of x and y in each leaf
        + nearest_leaf = least_eucledian_distance(each(xy_means_of_leaves) and (tx,ty))  
        + Run nb on nearest_leaf and calculate accuracy

Data

I used diabetes and iris to test my hypothesis. Other datasets are on their way. Lot of preprocessing needs to be done.

Initial projection of diabetes on xy-plane:

After generating leaves, xy projection of mean of each leafs:

Initial projection of iris on xy-plane:

After generating leaves, xy projectin of mean of each leafs:

Analysis

>>close 10
+test: [6.1, 2.8, 4.7, 1.2, '2']
closest leaf: 10 : [[6.2, 2.2, 4.5, 1.5, '2'], [6.3, 3.3, 4.7, 1.6, '2'],
[6.0, 2.2, 4.0, 1.0, '2'], [5.4, 3.0, 4.5, 1.5, '2'], [5.9, 3.0, 5.1, 1.8, '3'],
[7.0, 3.2, 4.7, 1.4, '2'], [5.8, 2.7, 5.1, 1.9, '3'], [5.9, 3.2, 4.8, 1.8, '2'],
[5.5, 2.3, 4.0, 1.3, '2'], [6.0, 3.4, 4.5, 1.6, '2'], [5.8, 2.7, 5.1, 1.9, '3'],
[6.0, 2.2, 5.0, 1.5, '3']] len: 12
0.26461058269 norm value for $sepallength
1.08565813063 norm value for $sepalwidth
5.43565621149e-12 norm value for $petallength
0.0209937597598 norm value for $petalwidth
0.794035419022 norm value for $sepallength
0.75813597268 norm value for $sepalwidth
0.963579623489 norm value for $petallength
0.913012880861 norm value for $petalwidth
likelyhood: {'3': -33.02818692221201, '2': -2.3785944862966026}
want: 2 got: 2

There is a problem

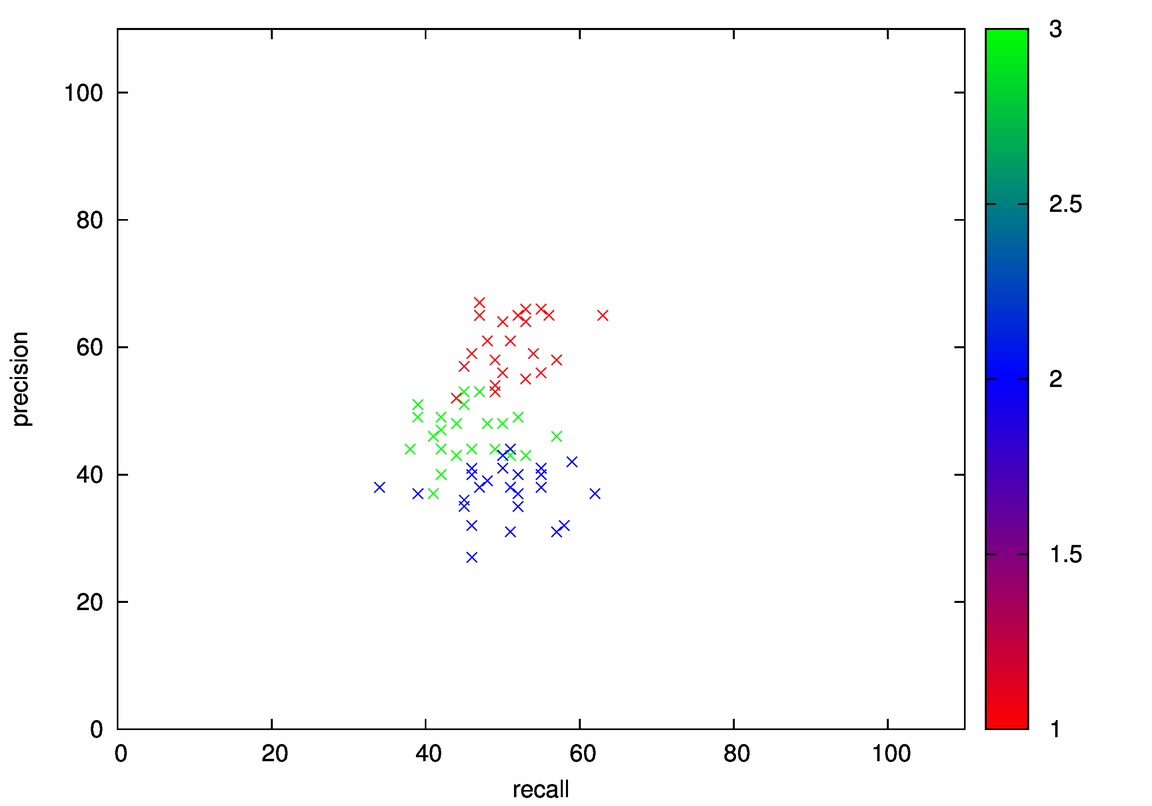
If the dataset has a low frequency class values, then accuracy might not be a good factor for evaluation.

We need to use "precision" and "recall" which are class specific and can be used to evaluate predictors.

Remember Abcd.py??

Results

After running the hypothesis for accuracy, the output is as follows:

Diabetes:

nb
67.97 68.63 69.28 69.93 71.24 71.24 72.55 73.2 73.86 
73.86 74.51 74.51 74.51 74.51 75.16 75.82 75.82 76.47
77.12 77.12 77.12 77.78 81.05 81.05 82.35 

nb-tree
39.87 41.83 42.48 43.14 43.14 45.75 46.41 47.06 47.71
48.37 49.67 50.33 50.33 50.98 50.98 50.98 50.98 51.63
51.63 52.29 52.29 54.25 54.25 54.25 54.9

Iris:

nb
86.67 90.0 90.0 90.0 93.33 93.33 93.33 93.33 93.33 93.33
93.33 96.67 96.67 96.67 96.67 96.67 96.67 100.0 100.0 100.0
100.0 100.0 100.0 100.0 100.0

nb-tree
73.33 73.33 73.33 73.33 73.33 76.67 76.67 76.67 80.0 80.0
80.0 83.33 83.33 86.67 86.67 86.67 86.67 86.67 86.67 90.0
90.0 93.33 93.33 93.33 93.33

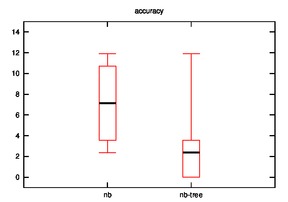
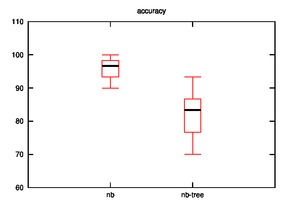
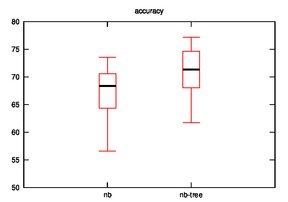
• Good: Image, Iris, Diabetes, Wine
• Bad: Cmc, Soybean

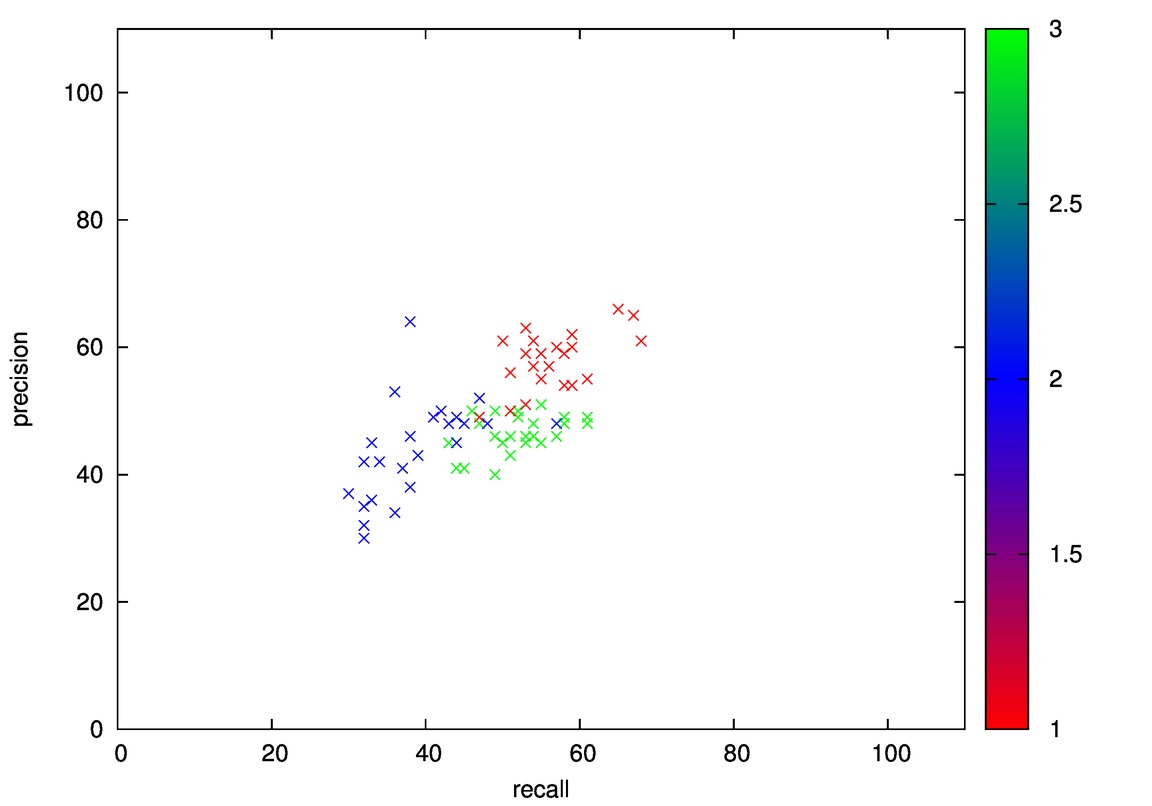
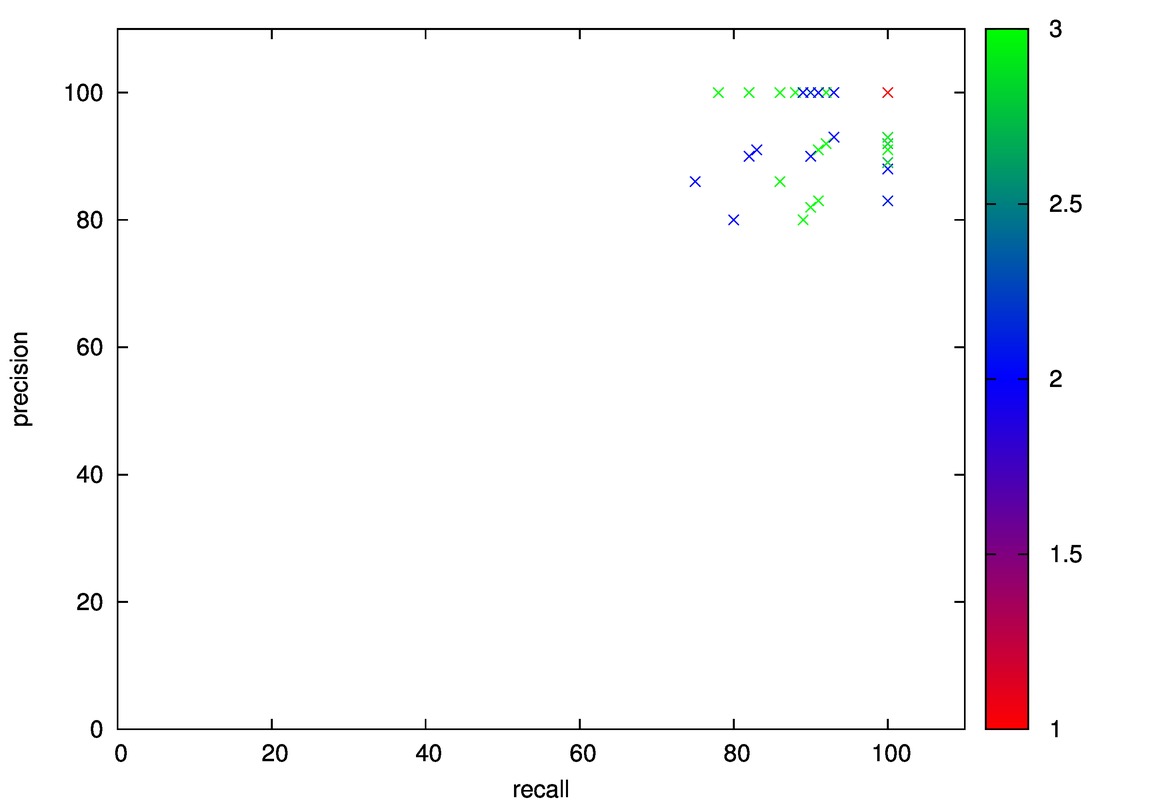
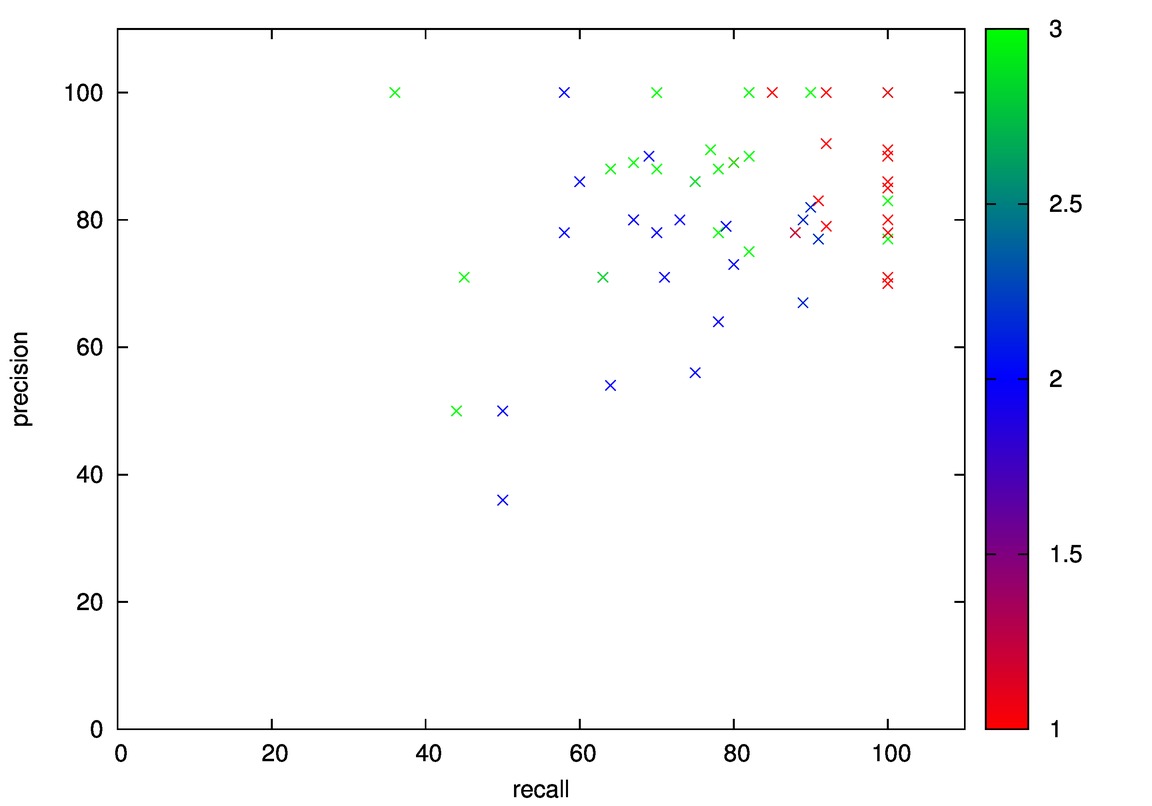
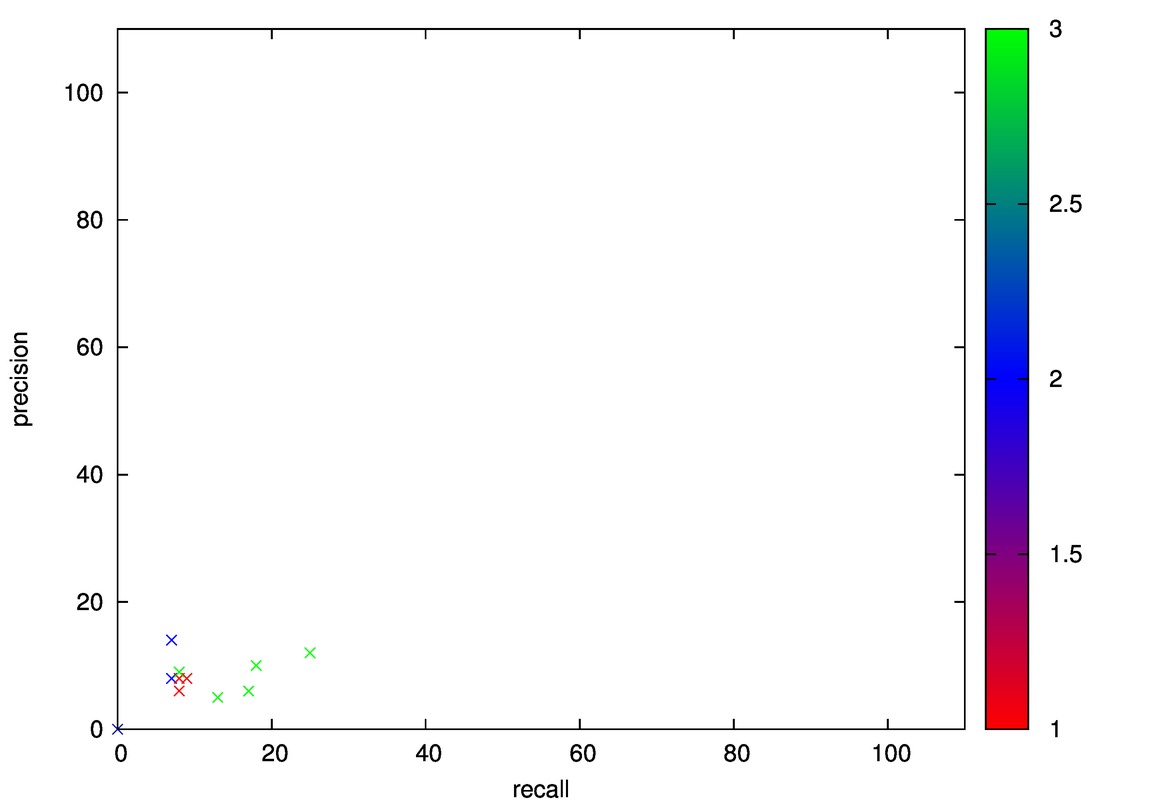
• Good: Wine, Cmc
• Bad: Iris

Discussion

As we can observe, the effectiveness of naive bayes is decreased in few cases and improves sometimes when the hypothesis is implemented.

Many cases are possible:

1. Our initial assumption that similar rows are closer on xy-plane may or may not be true.
2. The naive bayes is implemented on leaves rather than on nodes which may be decreasing it accuracy.
3. In other words, the leaf that we consider as closest for a test row may not be so close?
4. UPDATE: This is not valid as the distance calculation is tested in various hypothesis.
5. Low frequency class problem?
6. Datasets may not be effective for this case.

Future work

• I would like to test the hypothesis by running naive bayes at nodes instead of leaves by recursively traversing the tree till I get a good node of similar rows.

• Also, as the hypotheses is tested only on 6 datasets, I would like to test it on varying sets of data and check its effectiveness.

Conclusion

The naive bayes tree may not be effective when predictor is run on leaves of tree. The assumption that nb is more effective when it is run on similar data may not hold true.